We’re trying to figure out how to scale the space frame members to their maximum potential size given their proximity to the control surfaces, and then fill in the intermediate spaces with smaller scaled members. I think three or four scales max is ideal. Then we will add connection members between the space frame and the surfaces. We’re also working on having the space frame defined by two different surfaces to gain variability in the thickness, and defining new parameters for tesselation.
Testing Parametric Tesselation at Larger Scales
This is a test of the 2/3/6 surface tesselation on a larger surface. The file took approximately 15 minutes to calculate.
Surfaced 2/3/6 Tesselation Detail
The tesselation / space frame script we have been developing is now working flawlessly on any surface. We’re now working on architecturalizing the output, adding variability, multiple surfaces, and materiality.
Testing Tesselation
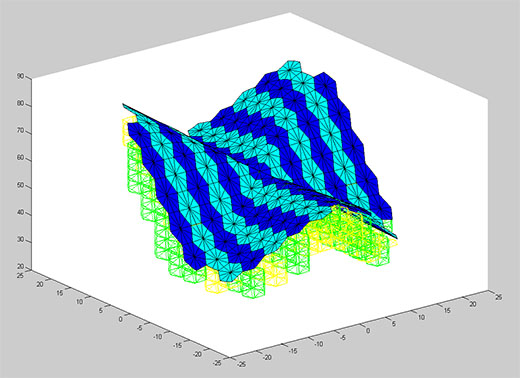
A detail view of a 2/3/6 tesselation sitting on a pruned space frame. The gap between the frame and the surface will be filled with custom members (we’re developing this now). We’re also working on a script that allows the hex crystals to move between scales where diagonal connections allow for larger crystals. The space frame members will scale to their largest optimal size given the surface boundary.
2/3/6 Tesselation
We’ve gotten the tesselation integrated into the approximation function now. We are using a 2/3/6 tesselation scheme that aligns in plan with our hex crystal space frame.
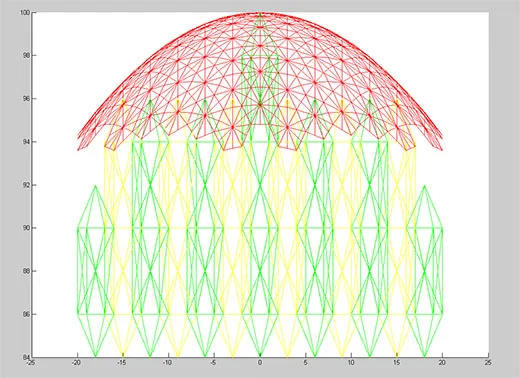
Optimizing Hex Crystal Geometry
We’ve modified the hex crystal geometry to be symmetrical vertically and added a bit of differentiation so we can see what’s happening at the surface a bit more clearly.
Ruled Surface on Complex Space Frame
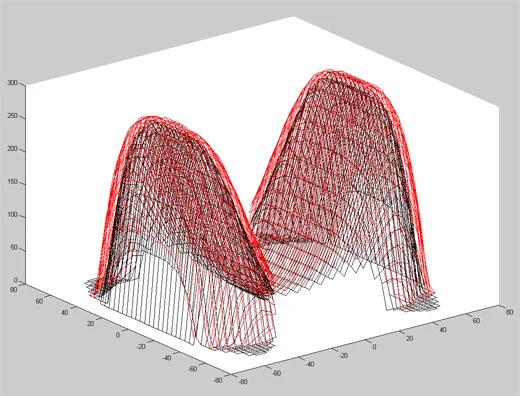
Here we are testing the potential for a ruled surface on a more complex spaceframe. The ruled surface is intersecting with the framing modules, so we need to develop another set of rules to offset surfaces based on this degree of intersection. We are also starting to investigate other tesselation methods that could work in concert with the spaceframe approximations.
Approximation With Dodecahedron Space-Frames
Now that we are able to approximate any surface with a dodecahedron space-frame, we are moving towards methods of inserting surficial variability to more closely approximate a particular shape. These screen shots arelooking at the potential of offsetting a ruled surface from the structural frame.
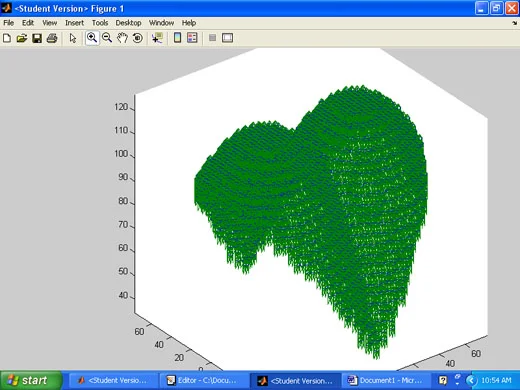
Heart Approximation
Our approximation function is now running relatively well. The script allows us to approximate any surface with a scalable dodecahedron module.
Crystalline Framing Module
In order to approximate a surface with geometric members, we must design something that can be repeatable in multiple vectors. We are thinking this crystalline form could be the basic geometry (the perspective is skewed, all of the triangles are equilateral).
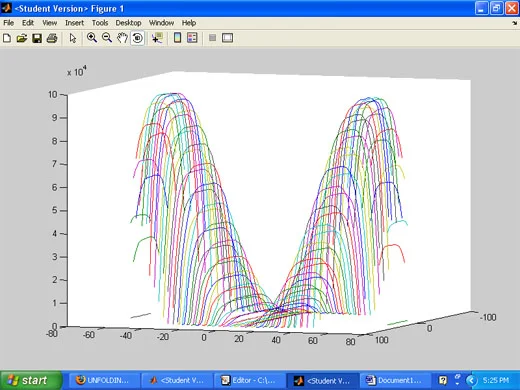
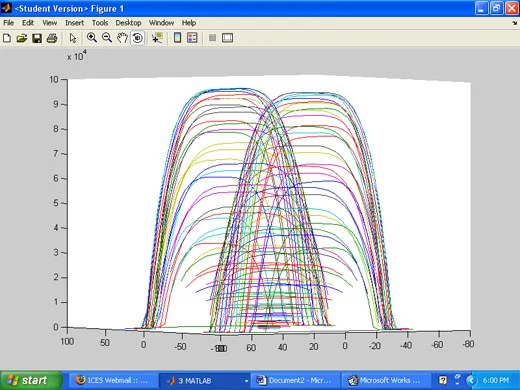
Surface Function
We are experimenting with MATLAB to generate surface functions with the intent of being able to produce complex surface and structural systems.
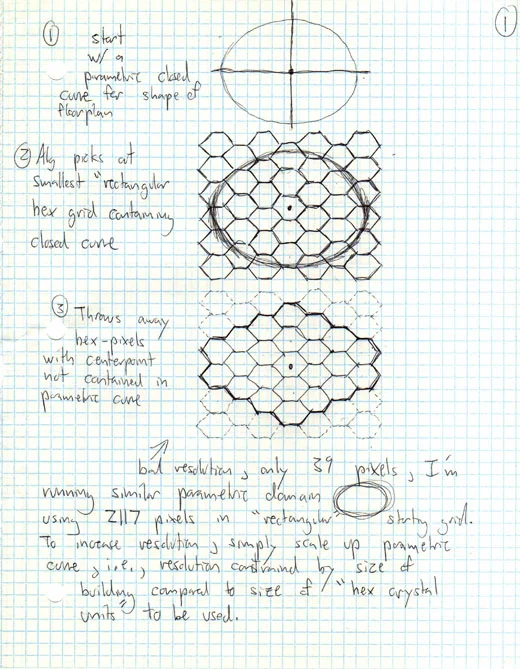
Hex Cloud Surface Approximation Concept
Parametric Domain
I think we are very close to getting our surface approximation script to work.
Surface Approximation with Dodecahedrons
Hyperbolic Tesselations
I stumbled onto these hyperbolic planar tesselations as I was researching different tesselation strategies for a project I’m developing. I asked my friend Alex Mollere, a Phd. candidate in applied mathematics at UT Austin, to explain:
… that’s the poincare disc model for the hyperbolic plane, a model for the space satisfying the postulates of the non-euclidean hyperbolic geometry in which infinitely many different lines may pass through a point P not on a line l without intersecting l, i.e., there is more than one line parallel to another given line. lines (i.e. the analog of “straight lines” in Euclidean plane) are the arcs of circles intersecting the poincare disc such that the angle between the boundary of the disc and the segment of the circle intersecting it is 90 degrees. The tesselations (just like in the Euclidean plane) are formed by segments of these lines. the dual tesselation is formed by the line segments intersecting the line segments of the original tesselation at 90 degrees, as you truncate the corners of the polygons forming the original regular tesselation, it gradually becomes its dual.