Cloudform

I've always been frustrated by the fact that two dimensional projected patterns deform as they map over a given shape rather than respond intelligently to the geometry of the shape. What I wanted to do with Cloudform was to make a script that would map a geometrically consistent pattern on the surface of a complex form. It is simple in concept, harder in execution. After a bit of thought I realized the problem could be solved in a way similar to how faces are mapped in animation. By projecting a two dimensional pattern onto a topologically identical but flattened version of the form, then reassembling the form, the pattern actually folds with the form rather than distorts around it.

Fractalizer Two

I've been playing around with an updated version of Fractalizer, a MEL script we wrote at Bureau V that produces a field of fractals on any given geometry. This image shows a plane with four levels of fractal division both in line and solid form.

Slicer

Slicer is a script I’ve written that cuts random angles into any form. Variables adjust the range of angles, the location of projection, and the quantity of cuts.

More Fractals

Fractal Surface

A test of the fractal MEL script on a deformed surface.

MEL Scripting Fractals

I just wrote a MEL script that produces fractal organizations. The example above has three degrees of fractalization. I'm working on other variations.

Convex / Concave

These images are quick studies for an installation we’re working on for the Issay Miyake store using chromed hemispheres.

Increasing Complexity

Here is an iterative complexity experiment using the Bloom MEL script that I wrote a while back...

Super Surface

I'm working on a dynamically driven parametric surface for our installation at the Whitney.

Koala Randomization

This is a series of tests using our Koala MEL Script in conjunction with the new randomization selection tool in Maya.

Playing With Koala and Randomization

This perforations in this surface were made using our Koala MEL Script and Maya's randomization tool.

Variable Array Using Koala

We made these color + pattern + variation studies earlier today while testing Koala, a MEL Script we have been developing for some time.

Perforation Studies Using Wolford

Wolford is a MEL script I wrote that produces geometric primitives that contain a reciprocal relationship between form and perforation. The above renderings show a Wankel inspired torus with two slightly varied strategies. The left form has perforation with a bit of randomization whereas the right form is a consistent perforation based on the surface geometry.

Form Based Perforation Studies

I'm working on a MEL script that perforates a surface proportionately to its geometry.

Testing Beatrice

Surface Patterning

This has been sitting on my desktop for a while. I think gave up on whatever it was supposed to be — but It is still working for me. Maybe I’ll un-give up.

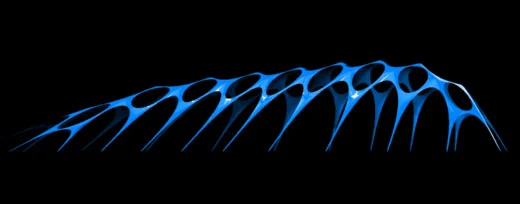
Catenary Topology

Taking my previous studies of a self optimizing topology as a starting point, I’m testing the effects of applied forces to create dynamic catenary arches. In this example the base topology is being drawn to a point of influence at approximately 15 deg above the surface. The surface doesn’t fully optimize its topology due to the localized forces acting along the ridgeline — something I need to resolve in the next iteration.

Beatrice

Beatrice is a MEL Script that produces radially gradient, scalar components aligned on a grid.

Surface Optimization Animation

This quick animation shows the self optimizing surface I’ve been working on. The clip shows local surface geometry automatically adjusting into the most efficient positions based upon the geometry of the edge control points.

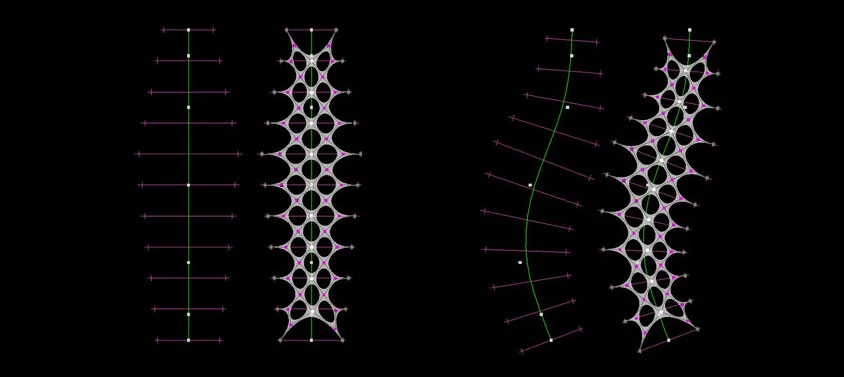
Dynamic Mesh Optimization

This study is something that takes up a number of issues that I’ve been interested in for some time: kinematic armatures, stockings, perforated meshes, and dynamic organization. The goal here is to develop a surface that optimizes its topology to any given form. The diagram above shows a lattice that controls the endpoints of the perforated surface and the resultant surface when these endpoints change position. It is very subtle in the two stages, but the perforations dynamically adjust their shape and position proportionally in respect to assumed material properties in the surface. This is a pretty simple example but the implications of this kind of optimized surface are really profound in my opinion. Not only does this approach solve the seemingly inherent “stopping problem” in dynamically driven architecture, but it provides a new kind of optimized geometry within a given formal organization.